2D Rayleigh-Bénard convection

One of the most striking features of Rayleigh-Bénard flow is the emergence of a large-scale convection roll. This roll is driven by small-scale thermal plumes detaching from the thermal boundary layers at the top and bottom. Remarkably, under certain conditions the large-scale convection roll can reverse its direction. For example, for Γ=1, Pr=4.3 (typical for warm water), and Ra=10⁸, spontaneous reversals of the large-scale convection roll occur (see figure 1 and Sugiyama et al., Phys. Rev. Lett. 105, 034503 (2010)), whereas for slightly larger Ra=5x10⁸ or slightly smaller Pr=0.7 (typical for gas) these reversals are suppressed. We found that the corner flows, which establish themselves next to the large-scale convection roll (see figure 1), play a central role: they are fed by the detaching thermal plumes, but also lose energy to the large-scale roll. Once the feeding process overwhelms the heat leakage, the corner flows can build up and eventually take over, leading to a reversal of the large-scale wind [1].

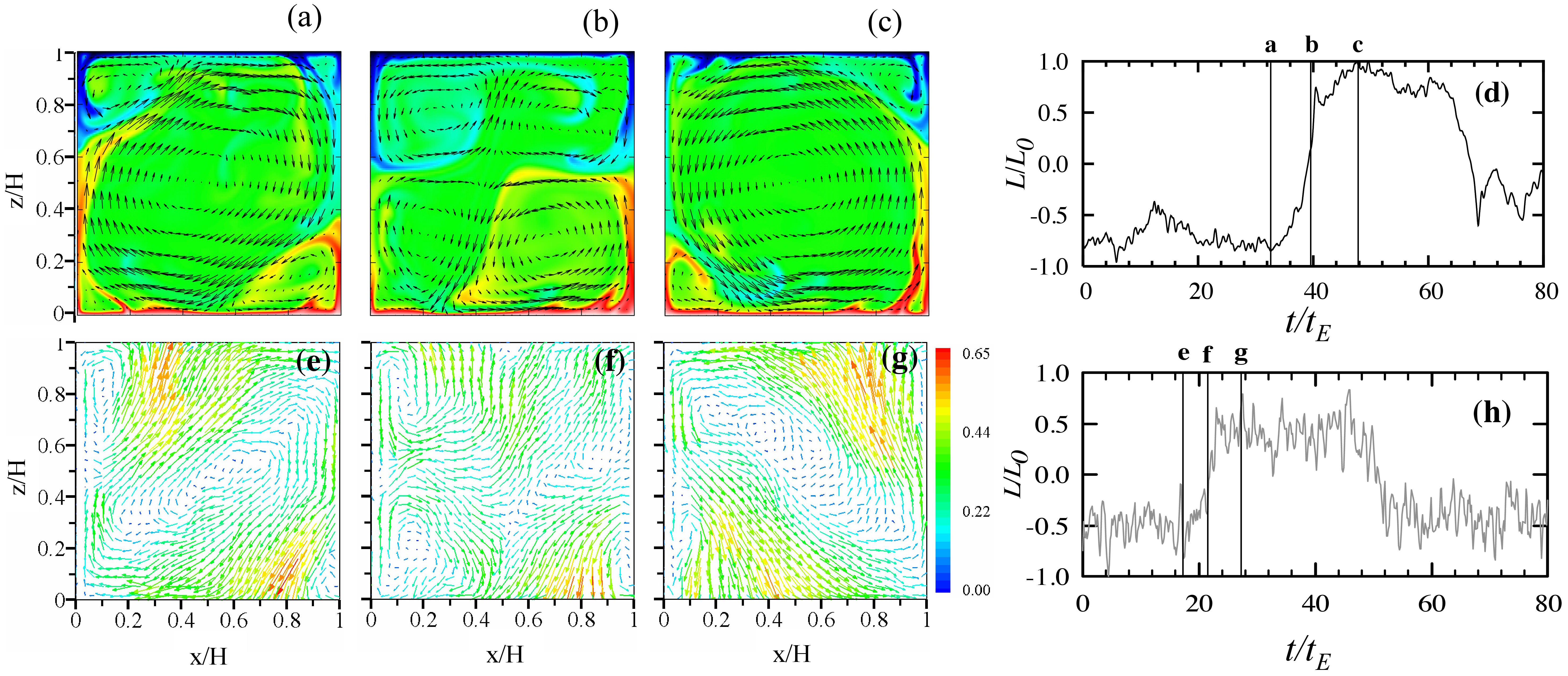
Figure 1. Top panel: Snapshots of the temperature (color) and velocity (arrows) fields and time trace of angular momentum from numerical simulations (Ra=10⁸ and Pr=4.3). Bottom panel: Snapshots of the velocity field and time trace of angular momentum from experiment (Ra=3.8x10⁸ and Pr=5.7). Panels (a), (b), and (c) show the instantaneous dimensionless temperature (T-T_t)/Δ. Panel (d) shows the temporal change of the dimensionless angular momentum L(t)/L₀, where L₀ is the maximum absolute value of L. The positive and negative signs indicate anticlockwise and clockwise circulations, respectively. Panels (e), (f), and (g) show the PIV-measured instantaneous velocity field, and panel (h) shows the normalized instantaneous angular momentum L(t)/L₀. The color bar indicates the velocity magnitude in cm/s. The numerical snapshots in panels (a), (b), and (c), and the experimental snapshots in panels (e), (f), and (g), show examples of the large-scale circulation before, during, and after a reversal process, as indicated in panels (d) and (h), respectively. Panels (b) and (f) show the key role played by the growth of the corner rolls in the reversal process. Figure from Sugiyama et al., Phys. Rev. Lett. 105, 034503 (2010).

In subsequent research [3] [4] we studied the aspect-ratio (Γ) dependence of the heat transfer (the dimensionless Nusselt number Nu) in turbulent two-dimensional Rayleigh-Bénard convection for different Rayleigh and Prandtl numbers. We found that Nu(Γ) shows a rich structure with sudden jumps and sharp transitions. We connect these structures to the way the flow organizes itself in the sample; see figure 2 and movie 1. Even at fixed control parameters, different turbulent states with different Nu can coexist, and the flow may or may not switch between them. In the latter case, the heat transfer depends on the initial conditions. This has implications for the comparison between two- and three-dimensional Rayleigh-Bénard convection, as discussed in Ref. [5].

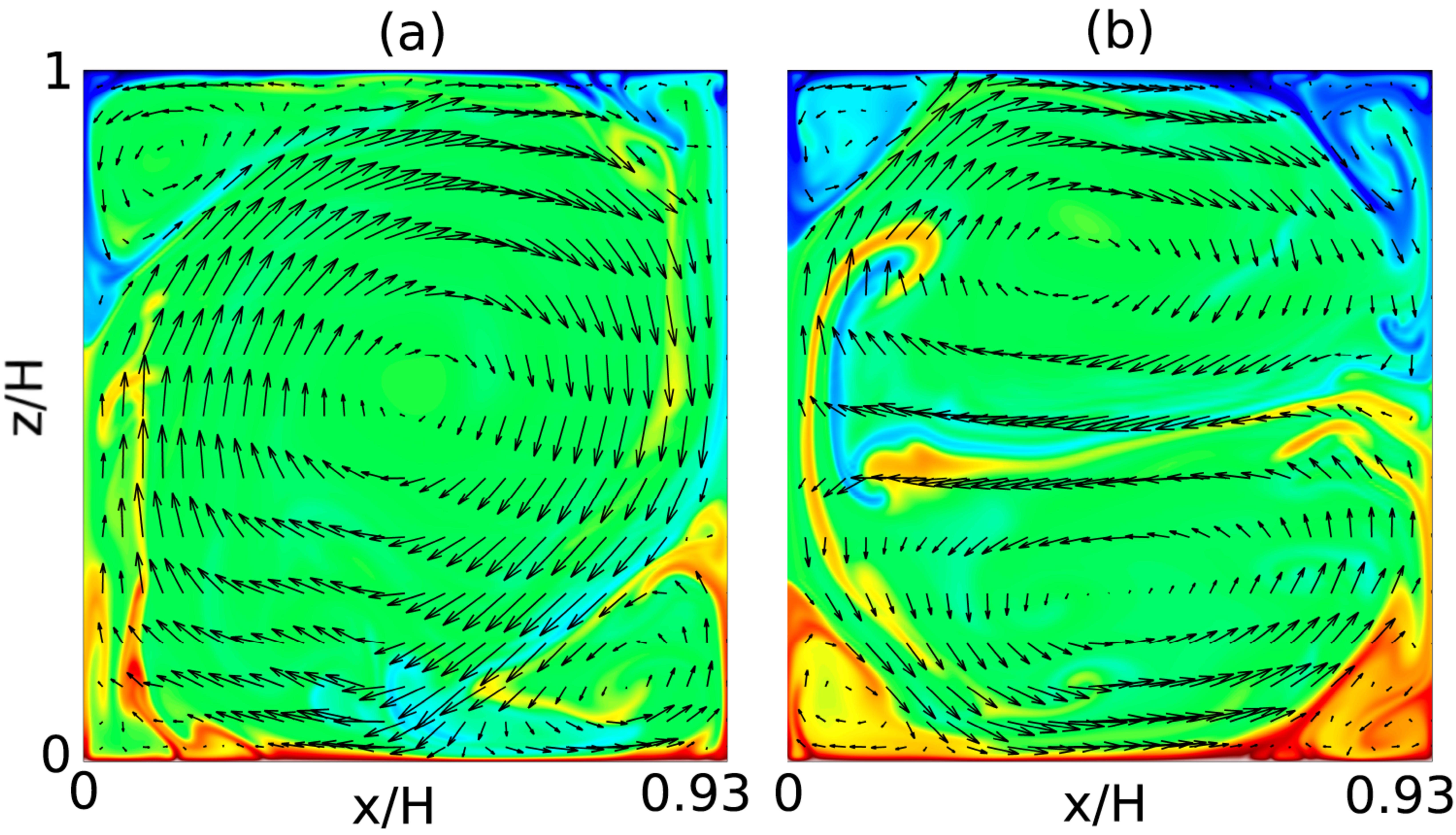
Figure 2. Two temperature snapshots for Ra=10⁹, Pr=4.3, and Γ=0.93. The system is either in the single-roll state (a) or in the double-roll state (b). Figure from Ref. [3].

Movie 1. Transition between the single-roll and double-roll states. The movie is published in the supplementary material of van der Poel, Stevens, and Lohse, Phys. Rev. E 84, 045303(R) (2011), where further movies are available.

References

7. X. Zhu, V. Mathai, R.J.A.M. Stevens, R. Verzicco, and D. Lohse,
   Transition to the ultimate regime in two-dimensional Rayleigh-Bénard convection,
   Phys. Rev. Lett. 120, 144502 (2018).
   Selected for the cover illustration.
8. X. Zhu, R.J.A.M. Stevens, R. Verzicco, D. Lohse,
   Roughness-facilitated local 1/2 scaling does not imply the onset of the ultimate regime of thermal convection,
   Phys. Rev. Lett. 119, 154501 (2017)
9. E.P. van der Poel, R.J.A.M. Stevens, D. Lohse,
   Comparison between two and three dimensional Rayleigh-Bénard convection,
   J. Fluid Mech. 736, 177-194 (2013).
10. E.P. van der Poel, R.J.A.M. Stevens, K. Sugiyama, D. Lohse,
    Flow states in two-dimensional Rayleigh-Bénard convection as a function of aspect-ratio and Rayleigh number,
    Phys. Fluids 24, 085104 (2012).
11. E.P. van der Poel, R.J.A.M. Stevens, D. Lohse,
    Connecting flow structures and heat flux in turbulent Rayleigh-Bénard convection,
    Phys. Rev. E 84, 045303(R) (2011).
12. Q. Zhou, K. Sugiyama, R.J.A.M. Stevens, S. Grossmann, D. Lohse, K.-Q. Xia,
    Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent Rayleigh-Bénard convection,
    Phys. Fluids 23, 125104 (2011).
    
13. K. Sugiyama, R. Ni, R.J.A.M. Stevens, T.S. Chan, S.-Q. Zhou, H.-D Xi, C. Sun, S. Grossmann, K.-Q. Xia, D. Lohse,
    Flow reversals in thermally driven turbulence,
    Phys. Rev. Lett. 105, 034503 (2010),
    Featured in the FOM News (in Dutch), 19 July 2010