High Rayleigh number thermal convection

Experimental and numerical studies of Rayleigh-Bénard convection are complementary to each other. For an accurate experimental measurement of the heat transfer a completely isolated system is needed. Therefore one can not visualize the flow while the heat transfer is measured. In direct numerical simulations one can simultaneously measure the heat transfer while the complete flow field is available. Therefore one can obtain data from simulations that can not be measured experimentally. Because experiments nowadays have reached a high level of accuracy these results can be used to verify the results obtained from simulations. And the simulations can then be used to explain effects observed in experiments. In direct numerical simulations it is very important to resolve all the relevant length scales of the flow and we showed that there is an excellent agreement between experiments and simulations when the resolution is sufficient [1], see figure 1a. Figure 2 shows a movie of the highest Rayleigh number simulation in the World [3]. The simulation is for Ra=2x10¹² with Pr=0.7 and is performed in a cylindrical Γ=0.5 cell on a computational mesh with 2701x671x2501 grid points. In later work we used direct numerical simulations to study the influence of the temperature boundary conditions at the sidewall on the heat transport in Rayleigh-Bénard convection [4].

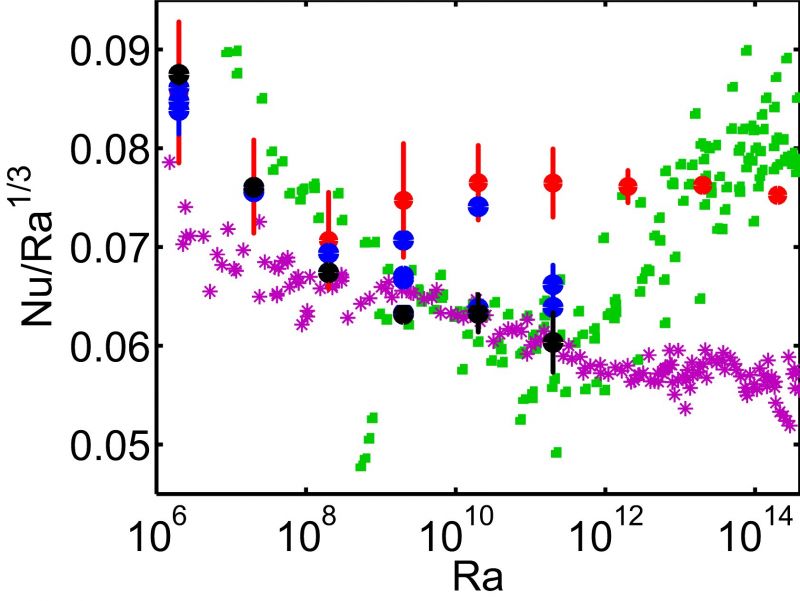
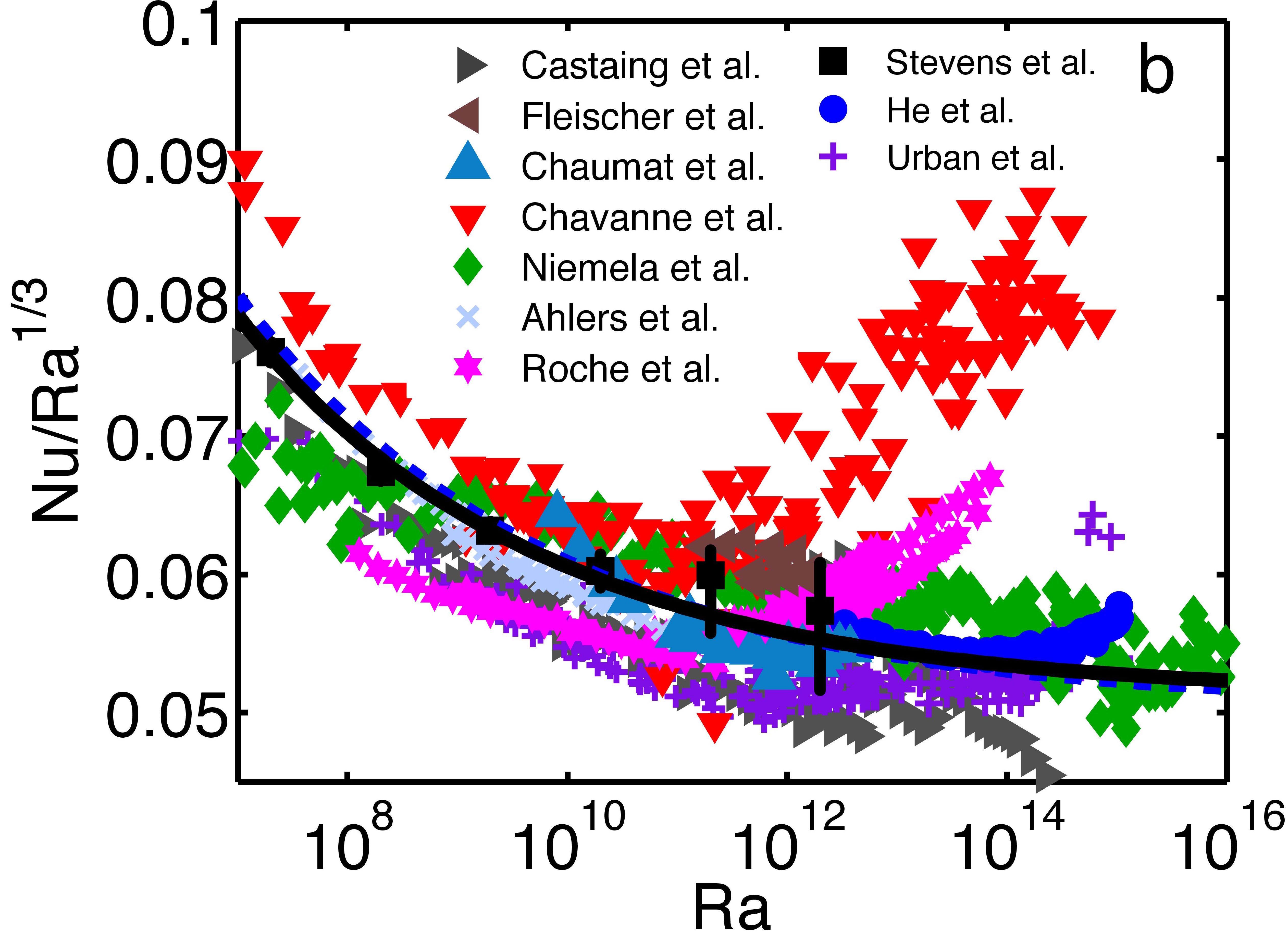
Figure 1: Compensated Nusselt number vs the Rayleigh number for Pr=0.7. (a) Purple stars are experimental data from Niemela et al. (2000) and the green squares are from Chavanne et al. (2001). The DNS results from Verzicco & Camussi (2003) and Amati et al. (2005) are indicated in red and high resolution results by R.J.A.M. Stevens, R. Verzicco, D. Lohse, J. Fluid Mech. 643, 495-507 (2010) are indicated by the black dots. When the vertical errorbar is not visible the error is smaller than the dot size. The results of underresolved simulations of this study are indicated by the blue dots. (b) Comparison between simulations, experiments, and the latest version of the Grossmann-Lohse theory published in the paper The unifying theory of scaling in thermal convection: The updated prefactors, J. Fluid Mech. 730 , 295-308 (2013). Good agreement is found up to Ra=10¹¹, but still unexplained differences are observed for higher Ra.

Movie 1: Movie of the temperature in a vertical cut for the simulation at Ra=2x10¹², Pr=0.7, and Γ=0.5. The dimensionless time is indicated in the top of the movie. This movie is rendered with a lower resolution for the website. Additional movies of this simulation can be found here.