Rotating Rayleigh-Bénard convection

An interesting variation of Rayleigh-Bénard convection is the case where the sample is rotated about the vertical axis, see figure 1 for a visualisation. The rotation speed of the system is defined by the Rossby number (Ro), which is an inverse rotation rate. This system is relevant to numerous astro- and geophysical phenomena, including convection in the Arctic Ocean, in the earth's outer core, in the interior of gaseous giant planets, and the outer layer of the Sun. Thus the problem is of interest in a wide range of sciences, including geology, oceanography, climatology, and astrophysics. Furthermore, the knowledge can be used in industrial applications. The key question we address is: How does rotation influence heat transport?

Figure 1: Flow visualization for Ra = 4.52 x 10⁹, Pr = 4.38, and 1/Ro = 3.33 in an aspect ratio Γ=1/2 sample. Figure taken from Ref. [8]. The simulation is published in the supplementary material of Stevens, Clercx, Lohse, Phys. Rev. E 86, 056311 (2012). This movie is rendered with a lower resolution for the website.

During my PhD we investigated the influence of rotation by using direct numerical simulations and laboratory experiments in the Turbulence and Vortex Dynamics group in Eindhoven in collaboration with Herman Clercx to measure the influence of rotation on heat transport. In the simulations we solve the incompressible Navier-Stokes and temperature equations with rotation in the Boussinesq approximation in a cylinder. Figure 2 shows that the heat transfer (the Nusselt number) can increase up to 20% for water when rotation is applied. To get this heat transport enhancement without rotation the temperature difference between the plates should be doubled! This heat transport enhancement is due to Ekman pumping, which leads to an enhanced suction of hot fluid out of the thermal BL and thus in a heat transport enhancement. This process is visualized in figure 1.

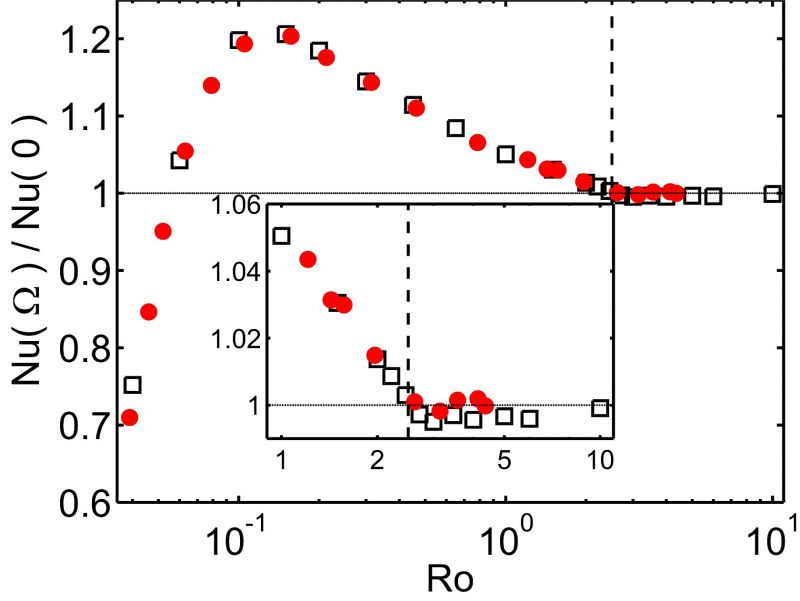
Figure 2: Normalized heat transfer as a function of the Rossby number for Ra=2.73x10⁸ and Pr=6.26. Red solid circles: experimental data from the group of Guenter Ahlers. Open black squares: numerical results. Figure based on the work presented in Stevens et al., Phys. Rev. Lett. 103, 024503 (2009).

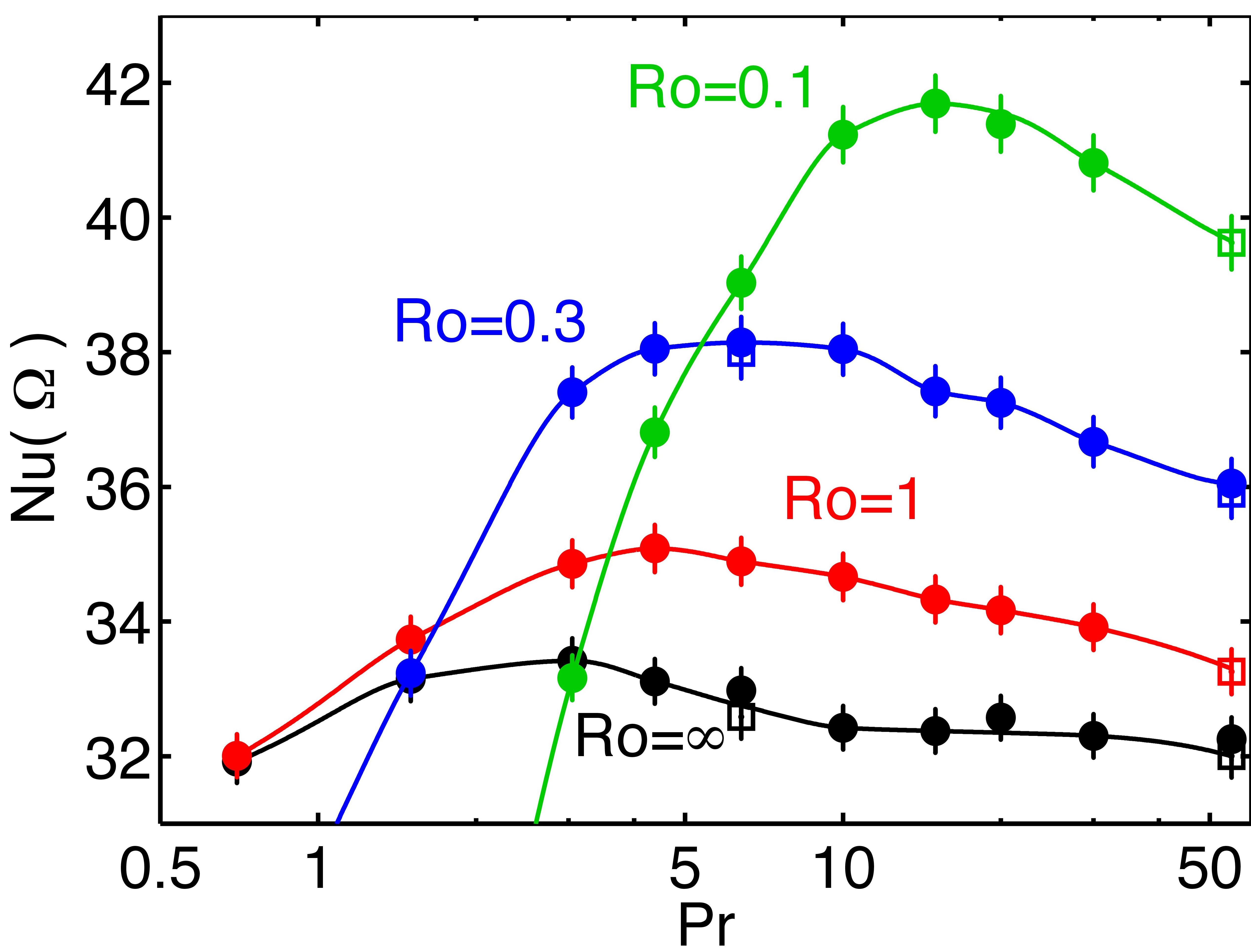
Figure 3: The heat transfer as a function of Pr on a logarithmic scale for Ra =1 x 10⁸. Black, red, blue and green indicate the results for Ro=∞ (no rotation), Ro=1.0, Ro=0.3 and Ro=0.1, respectively. The data obtained on the 193x385x385 (open squares) and the 129x257x257 grid (solid circles) are in very good agreement. Figure from Ref. [4].

Figure 3 shows that the heat transfer enhancement as function of the Prandtl number has an optimum. This suggests that the effect of Ekman pumping is determined by two different mechanisms. We find that in the low Prandtl number regime the effect of Ekman pumping is limited by the larger thermal diffusivity of the fluid. Therefore the heat that is sucked into the vortices spreads out in the middle of the cell and this limits the effect of the process. In the high Prandtl number regime the kinetic boundary layer becomes thicker with respect to the thermal boundary layer. Because the vortices are formed at the edge of the kinetic boundary layer the temperature of fluid that is sucked into the vortices decreases with increasing Prandtl and this limits the effect of Ekman pumping in the high Prandtl number regime. A visualisation of these vortices close to the plates is shown in figure 4.

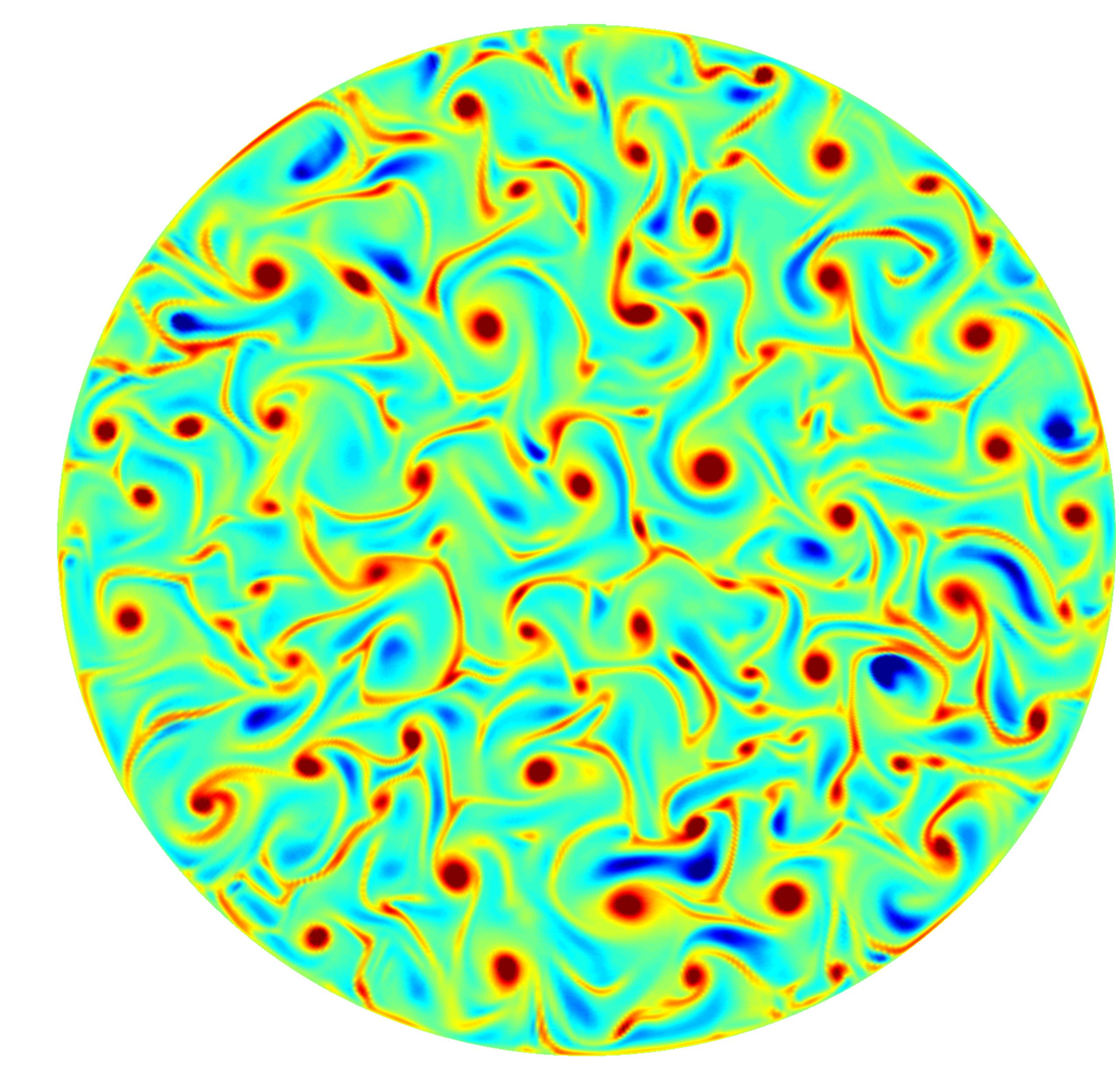
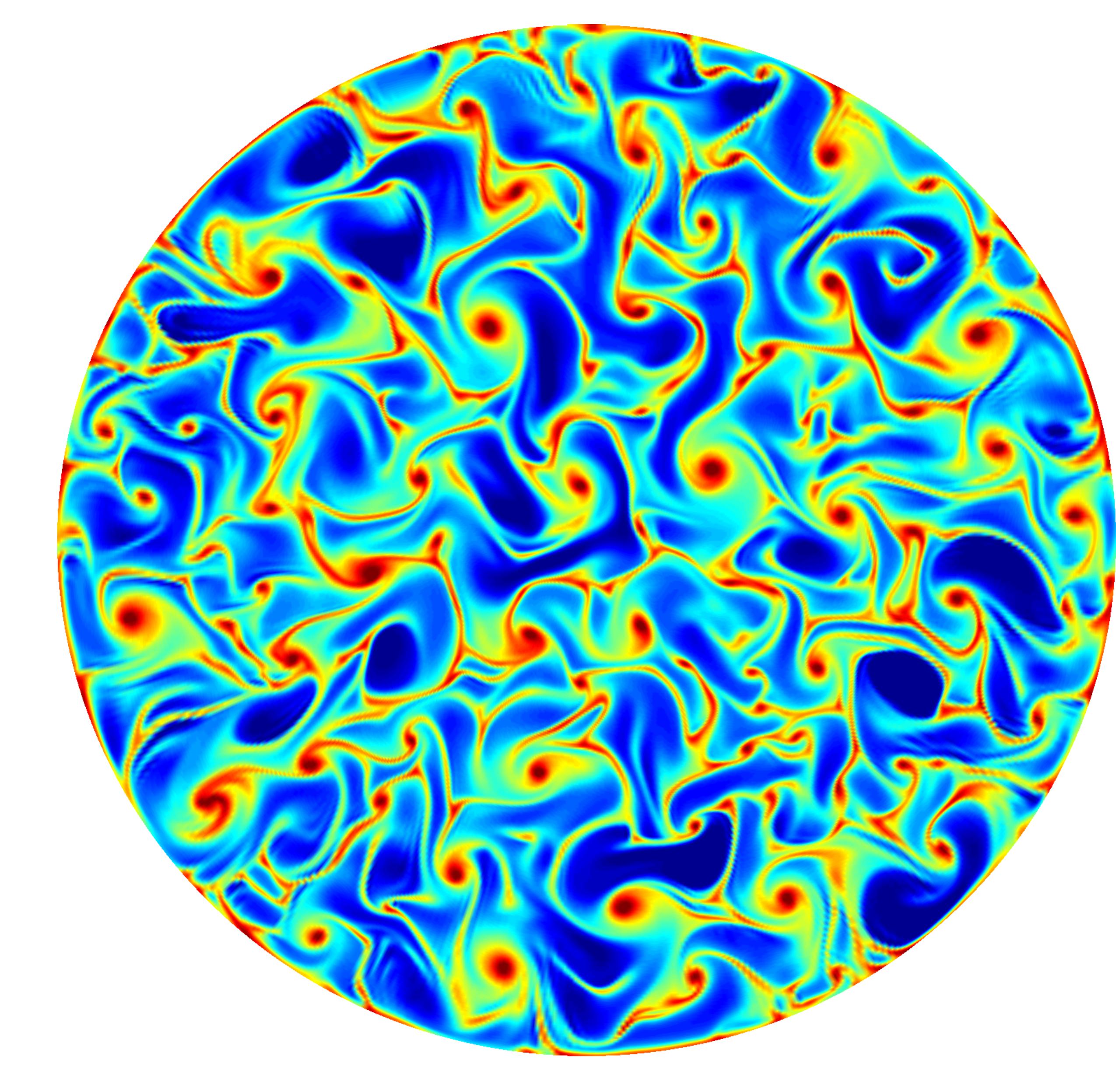
Figure 4: Visualization of the vertical velocity (left plot) and temperature (right plot) fields at the kinetic BL height for Ra=2.91x10⁸, Pr=4.38, 1/Ro=5, and Γ=2. Note that there is a strong correlation between the areas where the strongest vertical velocity and highest temperatures are found, namely, in the vortices. Red and blue indicate upflowing (warm) and downflowing (cold) fluid. Figure from Ref. [6].