Taylor-Couette turbulence

Taylor-Couette flow, i.e. the flow in the gap between two independently rotating coaxial cylinders, see figure 1, is among the most investigated problems in fluid mechanics, due to its conceptional simplicity and to applications in process technology. Just as for Rayleigh-Bénard convection the system is:
(i) mathematically well-defined by the Navier-Stokes equations and the appropriate boundary conditions,
(ii) there exist exact global balance relations between the driving and the dissipation rate, and
(iii) the system is experimentally and numerically accessible with high precision due to the simple geometry

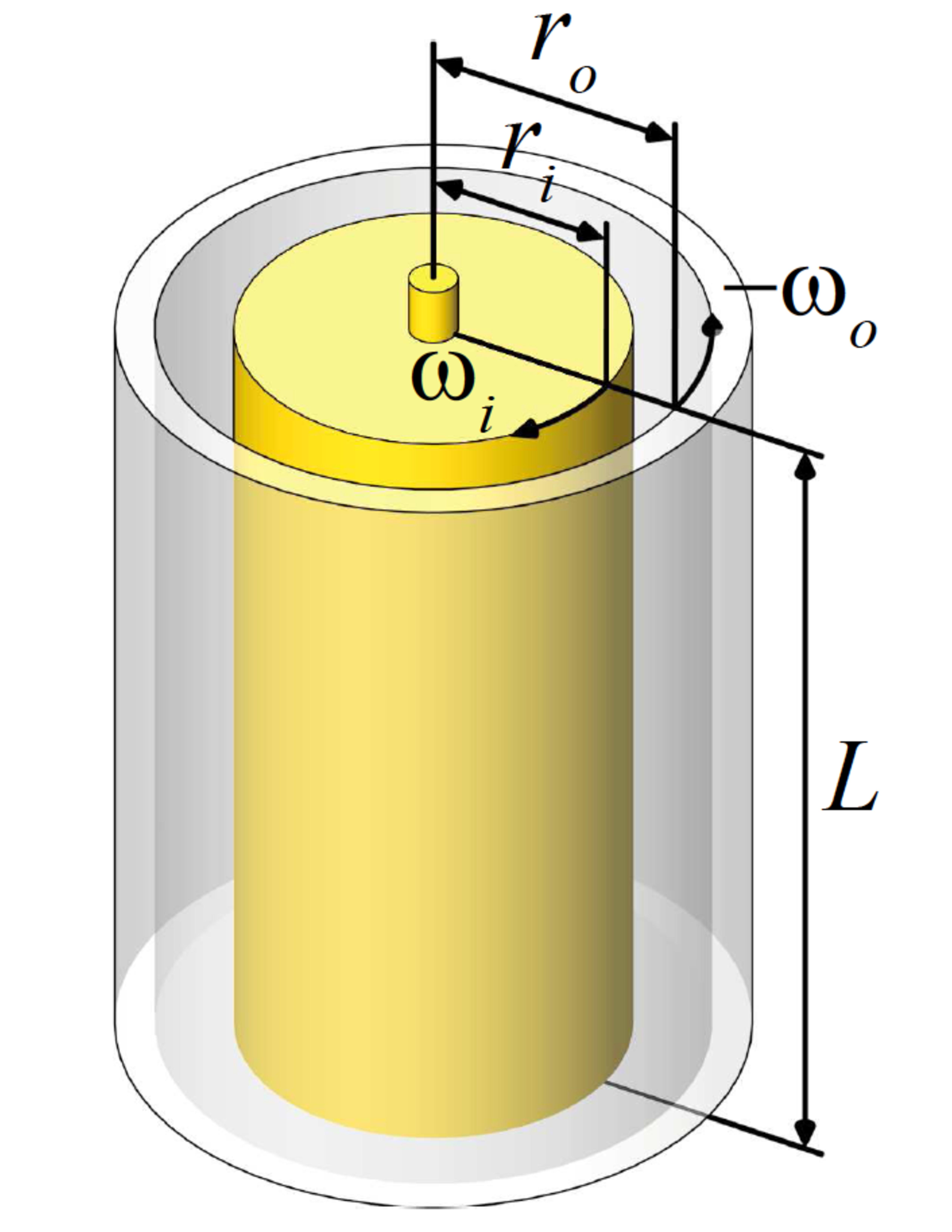
Figure 1: The Taylor-Couette system consists of two coaxial cylinders of length L. The inner cylinder has the radius r_i and the angular velocity ω_i, while the outer cylinder has the radius r_o and the angular velocity ω_o. Figure from Ref [1].

We [1] numerically simulated turbulent Taylor-Couette flow for independently rotating inner and outer cylinders, focusing on the analogy with turbulent Rayleigh-Bénard flow. Reynolds numbers of Re_i = 8 x 10³ and Re_o ± 4 x 10³ of the inner and outer cylinders, respectively, are reached, corresponding to Taylor numbers Ta up to 10⁸. Effective scaling laws for the torque and other system responses are found, see figure 2. Experiments with the Twente Turbulent Taylor-Couette (T³C) setup and with a similar facility in Maryland at very high Reynolds numbers have revealed an optimum transport at a certain non-zero rotation rate ratio a = ω_o / ω_i of about a_opt=0.33. For large enough Ta in the numerically accessible range we also find such an optimum transport at non-zero counter-rotation. The position of this maximum is found to shift with the driving, reaching a maximum of a_opt=0.15 for Ta=2.5x10⁷. Consistent with the experimental result that a_opt becomes approximately independent of the driving strength for large enough Reynolds numbers. In addition we investigated the angular velocity profiles and visualized the different flow structures for the various regimes.

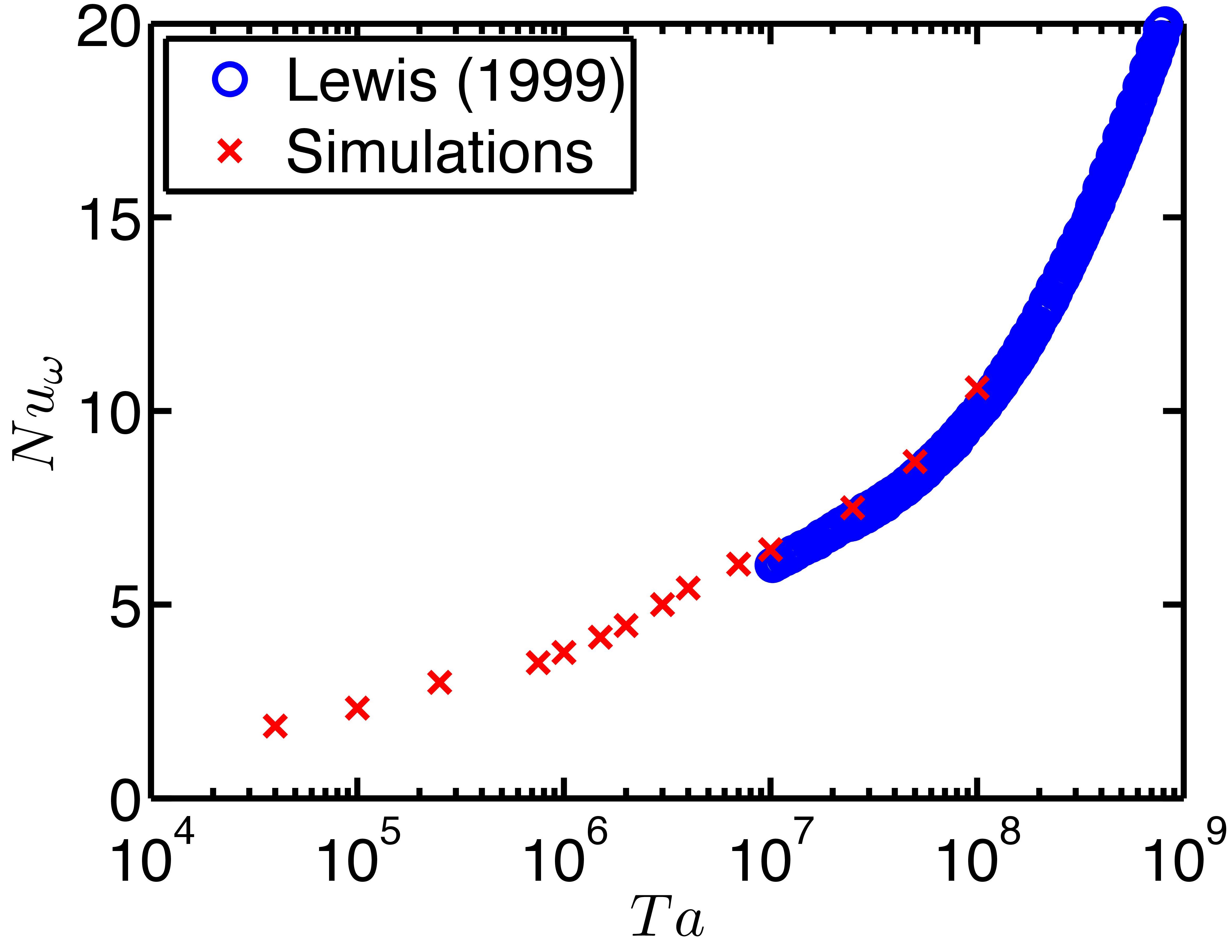
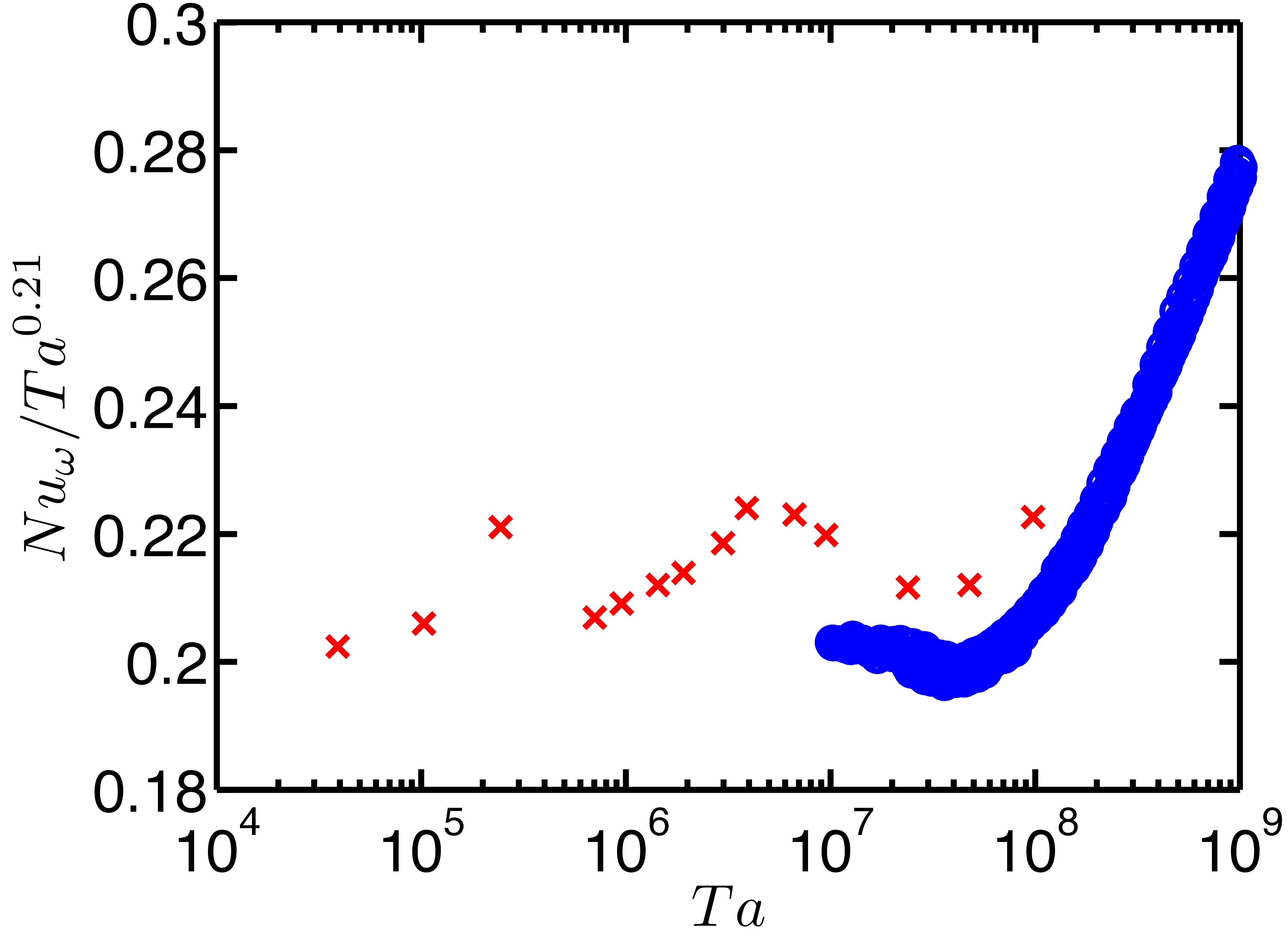
Figure 2: Left panel show the Absolute (Nu_ω) number and the right panel the compensated (Nu_ω / Ta^0.21) Nusselt number versus Ta for η=r_i/r_o=5/7. Experiments (dots) and the numerics agree in shape, but there is a slight shift between the data, which we attribute to the different boundary conditions in the lateral direction. Figure from Ostilla-Mónico et al. (2013).