Thermal convection

"Turbulence" is often used as synonym for "complexity". It is a multi-scale phenomenon, showing chaotic behavior both in space and time. But it is also a phenomenon in which self-organization plays a central role. Weather, climate, and ocean flow are all prime examples of both turbulence and complexity. The advantage in turbulence is that the underlying dynamical equations are well-known. The most important way to drive turbulent flow is thermally - think of the atmosphere or of ocean flow. The paradigmatic example for such buoyancy driven flow is the Rayleigh-Bénard system, i.e., a fluid-filled cell heated from below and cooled from above. Next to the aspect ratio, defined by width of the cell divided by its height L, the central control parameters of the system are the Rayleigh number Ra (the dimensionless temperature difference between bottom and top plate) and the Prandtl number Pr (the ratio between kinematic viscosity and thermal diffusivity).

Heat transfer in a Rayleigh-Bénard system can satisfactory be described by the Grossmann-Lohse (GL) theory. In the GL-theory the Prandtl-Blasius boundary layer theory for laminar flow over an infinitely large plate was employed in order to calculate the thicknesses of the kinetic and thermal boundary layers, the kinetic and thermal dissipation rates, and finally these results were connected with the Rayleigh and Prandtl number dependence of the Nusselt number. Because the dynamics of the Rayleigh-Bénard system depends on the location, i.e. in the boundary layers or in the bulk, where most dissipation takes place, the Ra-Pr parameter space can be divided in different regimes as is shown in figure 1.

The following topics are specifically addressed:
High Rayleigh number thermal convection
Rotating Rayleigh-Bénard convection
2D Rayleigh-Bénard convection

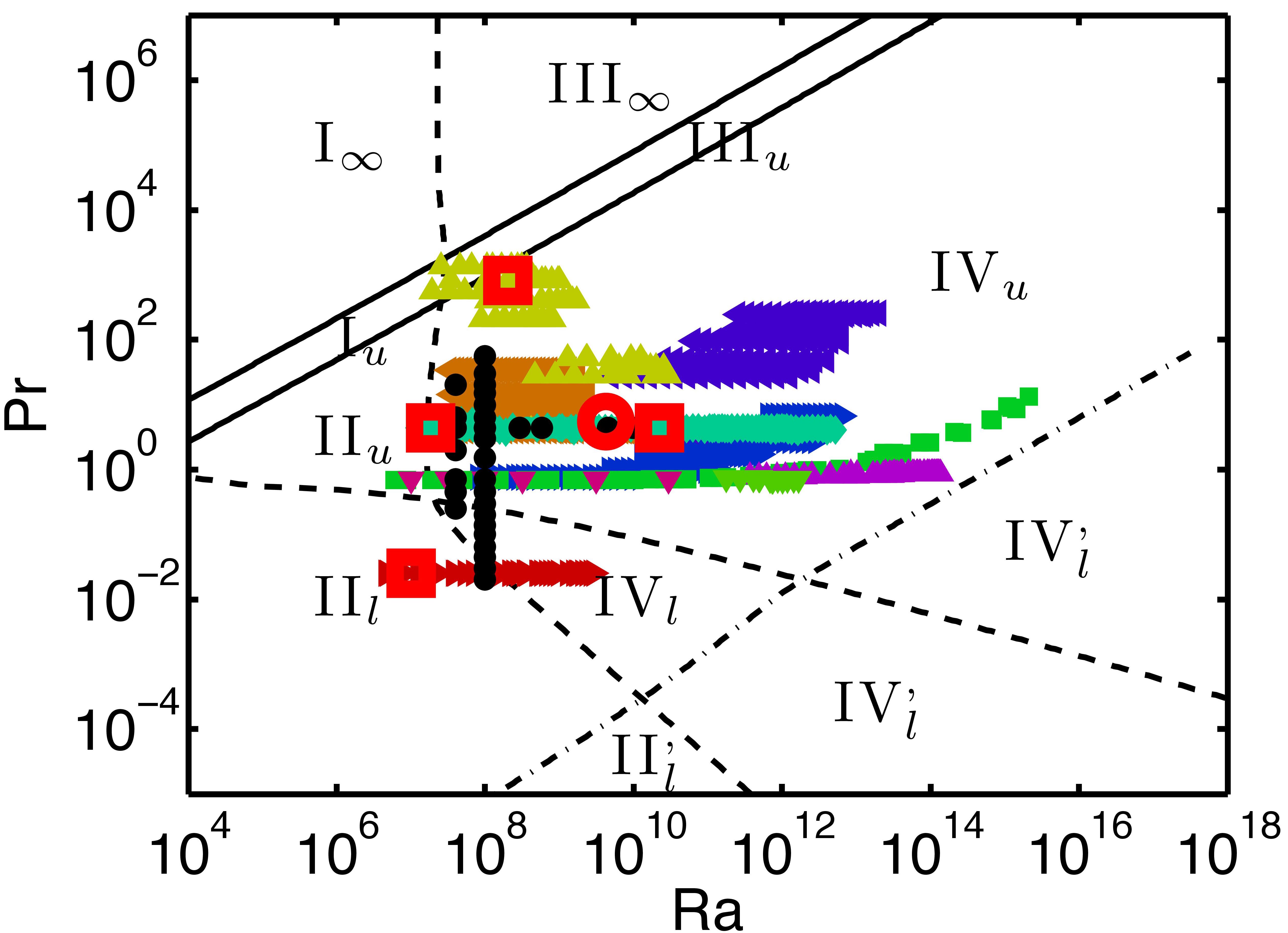
Figure 1: Phase diagram in Ra-Pr plane indicating the different turbulent regimes. The data points indicate where Nu has been measured or numerically calculated, figure from Ref. [3] where details about the shown data points can be found.